迪杰斯特拉 (Dijkstra) 算法

基本思想

1. 通过 Dijkstra 计算图 G 中的最短路径时，需要指定一个起点 D (即从顶点 D 开始计算)。
2. 此外，引进两个数组 S 和 U。S 的作用是记录已求出最短路径的顶点 (以及相应的最短路径长度)，而 U 则是记录还未求出最短路径的顶点 (以及该顶点到起点 D 的距离)。
3. 初始时，数组 S 中只有起点 D；数组 U 中是除起点 D 之外的顶点，并且数组 U 中记录各顶点到起点 D 的距离。如果顶点与起点 D 不相邻，距离为无穷大。
4. 然后，从数组 U 中找出路径最短的顶点 K，并将其加入到数组 S 中；同时，从数组 U 中移除顶点 K。接着，更新数组 U 中的各顶点到起点 D 的距离。
5. 重复第 4 步操作，直到遍历完所有顶点。

算法图解

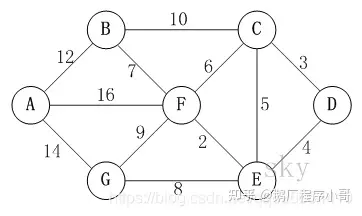
以上图为例，来对迪杰斯特拉进行算法演示 (以顶点 D 为起点)。

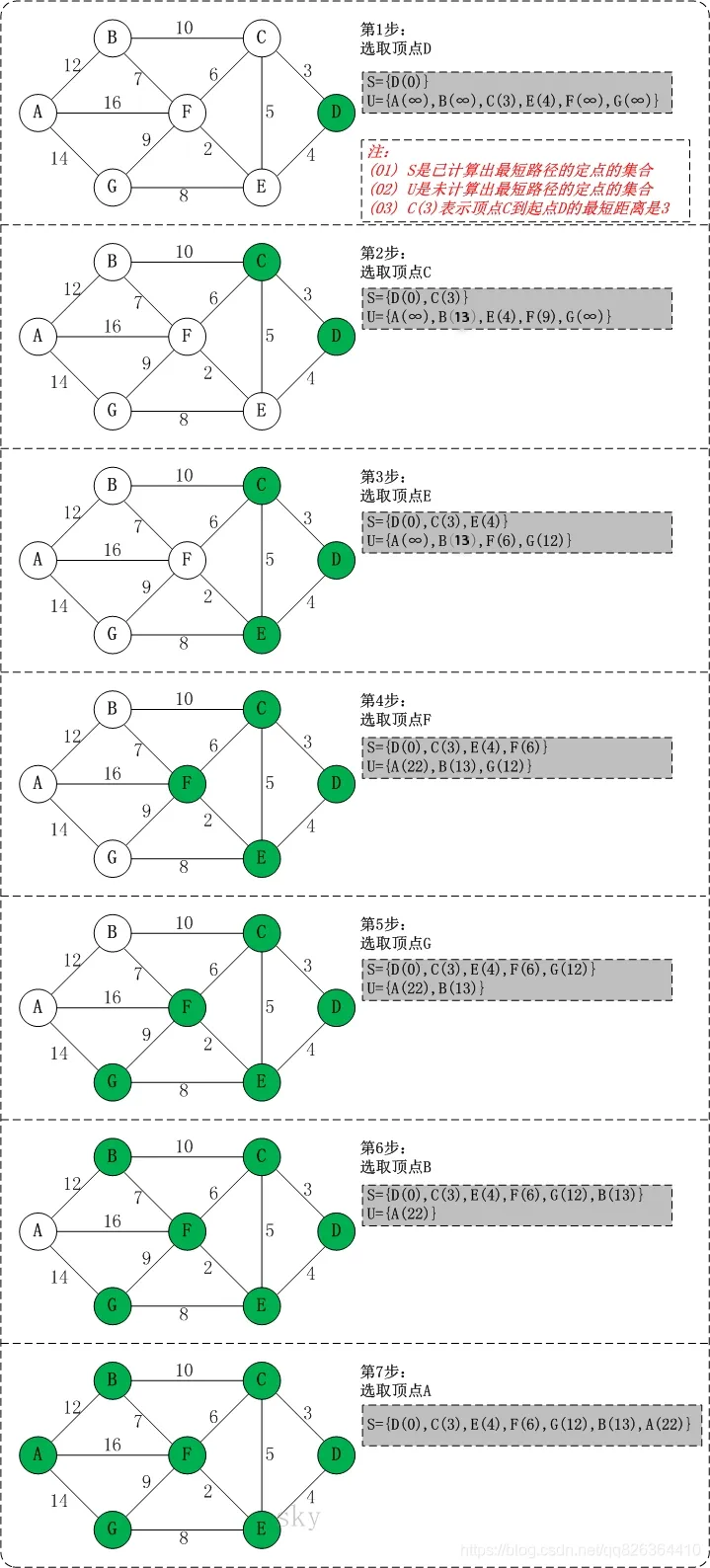
初始状态：S 是已计算出最短路径的顶点集合，U 是未计算除最短路径的顶点的集合！

第 1 步：将顶点 D 加入到 S 中。
此时，S={D (0)}, U={A (∞),B (∞),C (3),E (4),F (∞),G (∞)}。 注：C (3) 表示 C 到起点 D 的距离是 3。

第 2 步：将顶点 C 加入到 S 中。
上一步操作之后，U 中顶点 C 到起点 D 的距离最短；因此，将 C 加入到 S 中，同时更新 U 中顶点的距离。以顶点 F 为例，之前 F 到 D 的距离为∞；但是将 C 加入到 S 之后，F 到 D 的距离为 9=(F,C)+(C,D)。
此时，S={D (0),C (3)}, U={A (∞),B (13),E (4),F (9),G (∞)}。

第 3 步：将顶点 E 加入到 S 中。
上一步操作之后，U 中顶点 E 到起点 D 的距离最短；因此，将 E 加入到 S 中，同时更新 U 中顶点的距离。还是以顶点 F 为例，之前 F 到 D 的距离为 9；但是将 E 加入到 S 之后，F 到 D 的距离为 6=(F,E)+(E,D)。
此时，S={D (0),C (3),E (4)}, U={A (∞),B (13),F (6),G (12)}。

第 4 步：将顶点 F 加入到 S 中。
此时，S={D (0),C (3),E (4),F (6)}, U={A (22),B (13),G (12)}。

第 5 步：将顶点 G 加入到 S 中。
此时，S={D (0),C (3),E (4),F (6),G (12)}, U={A (22),B (13)}。

第 6 步：将顶点 B 加入到 S 中。
此时，S={D (0),C (3),E (4),F (6),G (12),B (13)}, U={A (22)}。

第 7 步：将顶点 A 加入到 S 中。
此时，S={D (0),C (3),E (4),F (6),G (12),B (13),A (22)}。

此时，起点 D 到各个顶点的最短距离就计算出来了：A (22) B (13) C (3) D (0) E (4) F (6) G (12)。

代码实现

依据上述步骤思想进行实现即可，visited 数组表示已加入的顶点。

import java.util.*;

public class DijkstraAlgorithm {

    private static final int INF = Integer.MAX_VALUE;

    public static void dijkstra(int[][] graph, int source) {
        int vertices = graph.length;
        int[] distance = new int[vertices];
        boolean[] visited = new boolean[vertices];

        // 初始化距离数组为无穷大，除了起始顶点为0
        Arrays.fill(distance, INF);
        distance[source] = 0;

        for (int i = 0; i < vertices - 1; i++) {
            int minVertex = findMinDistanceVertex(distance, visited);
            visited[minVertex] = true;

            for (int j = 0; j < vertices; j++) {
                if (!visited[j] && graph[minVertex][j] != 0 && distance[minVertex] != INF &&
                        distance[minVertex] + graph[minVertex][j] < distance[j]) {
                    distance[j] = distance[minVertex] + graph[minVertex][j];
                }
            }
        }

        // 打印最短路径
        printShortestPaths(distance, source);
    }

    private static int findMinDistanceVertex(int[] distance, boolean[] visited) {
        int minDistance = INF;
        int minVertex = -1;

        for (int i = 0; i < distance.length; i++) {
            if (!visited[i] && distance[i] < minDistance) {
                minDistance = distance[i];
                minVertex = i;
            }
        }

        return minVertex;
    }

    private static void printShortestPaths(int[] distance, int source) {
        System.out.println("顶点\t\t最短距离");

        for (int i = 0; i < distance.length; i++) {
            System.out.println(source + " -> " + i + "\t\t" + distance[i]);
        }
    }

    public static void main(String[] args) {
        int[][] graph = {
                {0, 4, 0, 0, 0, 0, 0, 8, 0},
                {4, 0, 8, 0, 0, 0, 0, 11, 0},
                {0, 8, 0, 7, 0, 4, 0, 0, 2},
                {0, 0, 7, 0, 9, 14, 0, 0, 0},
                {0, 0, 0, 9, 0, 10, 0, 0, 0},
                {0, 0, 4, 14, 10, 0, 2, 0, 0},
                {0, 0, 0, 0, 0, 2, 0, 1, 6},
                {8, 11, 0, 0, 0, 0, 1, 0, 7},
                {0, 0, 2, 0, 0, 0, 6, 7, 0}
        };

        dijkstra(graph, 0);
    }
}

鸣谢

最短路径算法 - 迪杰斯特拉 (Dijkstra) 算法